A user friendly theory of chess magic bitboard numbers. At first, here are good sites to read on the web:
Chess programming wiki, Pradu, codeproject.net, Chessprogramming.net, an essay, and other.
People are lazy, they like it short. So, here it is.

What are the magic numbers

   Chess moves can be precomputed and, as so called, bitboard masks (big 64bit numbers) can be applied as ready data - avoiding slow loops throughout the chess board in time of actual playing. The magic lies in the nature that really there are such big numbers, multiplying occupancy by which, the program almost instantly gets all the legal only bishop/rook/queen moves. In a deep search, performance matters. Big win. A lot.

Workout of the problem

   At first, split everything into 64 squares. If we solve one square, then can solve all.
The next thing, split bishops (diagonals) and rooks (lines). Almost the same for both.

Clear the board and put, let's say, a bishop on E4. Now we see where bishop can move.
Then put some blocking pieces. We are interested in blue points only. Our pieces are blockers too. Ignore piece color.
Because we easily will cut them out later - with mask ~OurPieces. We are interested only to find the moves till blockers.
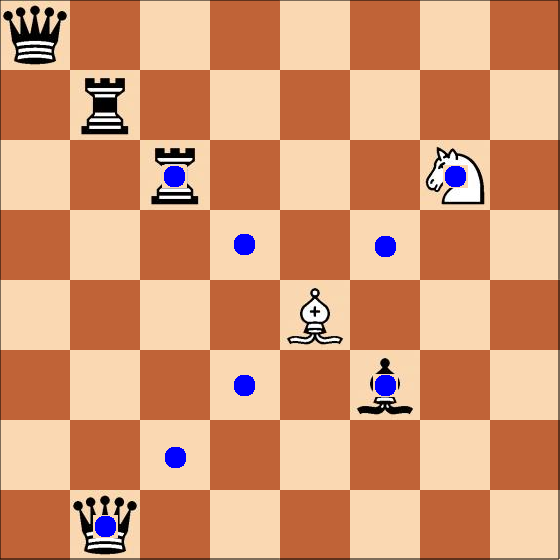Now imagine a large table with column of all possible blockers on the bishop diagonals. The other column is the result - legal moves. Permutations of occupancy - all combinations of pieces on diagonals, and resulting moves. Such list is only one, and it's long.

Blockers occupancy: A8, B7, C6, ....B1, ... all other cases...

Bishop can move: d5,f3,... accordingly legal moves cases...

Now we already have a database where to lookup.
Here is a tool to generate this table. Can mysql and have fun.

So,almost there. But we don't need a database. We want a fast math function, instantly working and fast.
f( occupancy of blockers pieces ) that gives us the legal moves for bishop on E4, nothing other.
It seems, there is no sequence of simple math operators +,-,*,/,%,~,^,>>,<<... that gives us the right result as a number. But we can combine math and data lookup to make it work anyway.


   Now insert a middle column - blank empty space. Call it "IndexOn". We will build our own index there.

Blockers: occupancy1 occupancy2 ... all other cases...

IndexOn:

Bishop can move: moveslist1 moveslist2 ... accordingly legal moves cases...

The IndexOn column can be large. The physical position of each record already is a numerated index. This index is as an array with length we afford. Now we start a searching processing that:
 1.clears column IndexOn;
 2.loops the blockers occupancy column and does a math function (later) that gives a number;
 3.use this number as a pointer in column IndexOn and remember the resulting chess moves (calculate and write - mark them). Sometimes pointer is used before.
 4.if all numbers don't overlap, or finds same chess moves, then the column is good and the Magic has happened! This means we got "the right key".
 5.if no success then repeat it all day long, go to 1.

Mainly the task is to find a table with enaugh free rows to put our move calculation only one time, as we know square,piece,blockers. It is possible to find fast math for a larger column, or much easier (more bits, less shiftNumber later). We have just transformed both columns to other dimension. Have built a specially indexed relation, as we need.
So, regenerate this "IndexOn" column when the chess program starts and legal chess moves on demand are ready to use.


   There is nothing better than multiplication. Gives a partly proportional number, partly random, fast enaugh.
And sequently applied >> function (right bit shift) simply transforms big number to short, as we need an index of an array only.
So,
   chess moves = TableIndexOn record [ (occupancy * MagicNumber) >> shiftNumber ]

These MagicNumber and shiftNumber can be found by full-scan. Just as described above: use random and try to apply. If not ok then repeat. Or use a ready tool or sources of strong chess engines. The magicgen tool available. Also on Github.


   Yee yee, there are inner square B2-G7 cases with same results. I don't care if list is little longer.
Also, there may be other fast math functions combined with bit-operators to calculate the index.
In fact, lots of calculations can be magic-number based, also moves of pawns, or whatever else.
That's it. Now can dive without support.